三角形角度计算公式（已知三角形三边长度，不利用余弦定理，怎么求角度呢？）

100次浏览发布时间：2024-10-14 09:37:28

已知△ABC，AB=6，BC=14，AC=10，求∠A的度数。

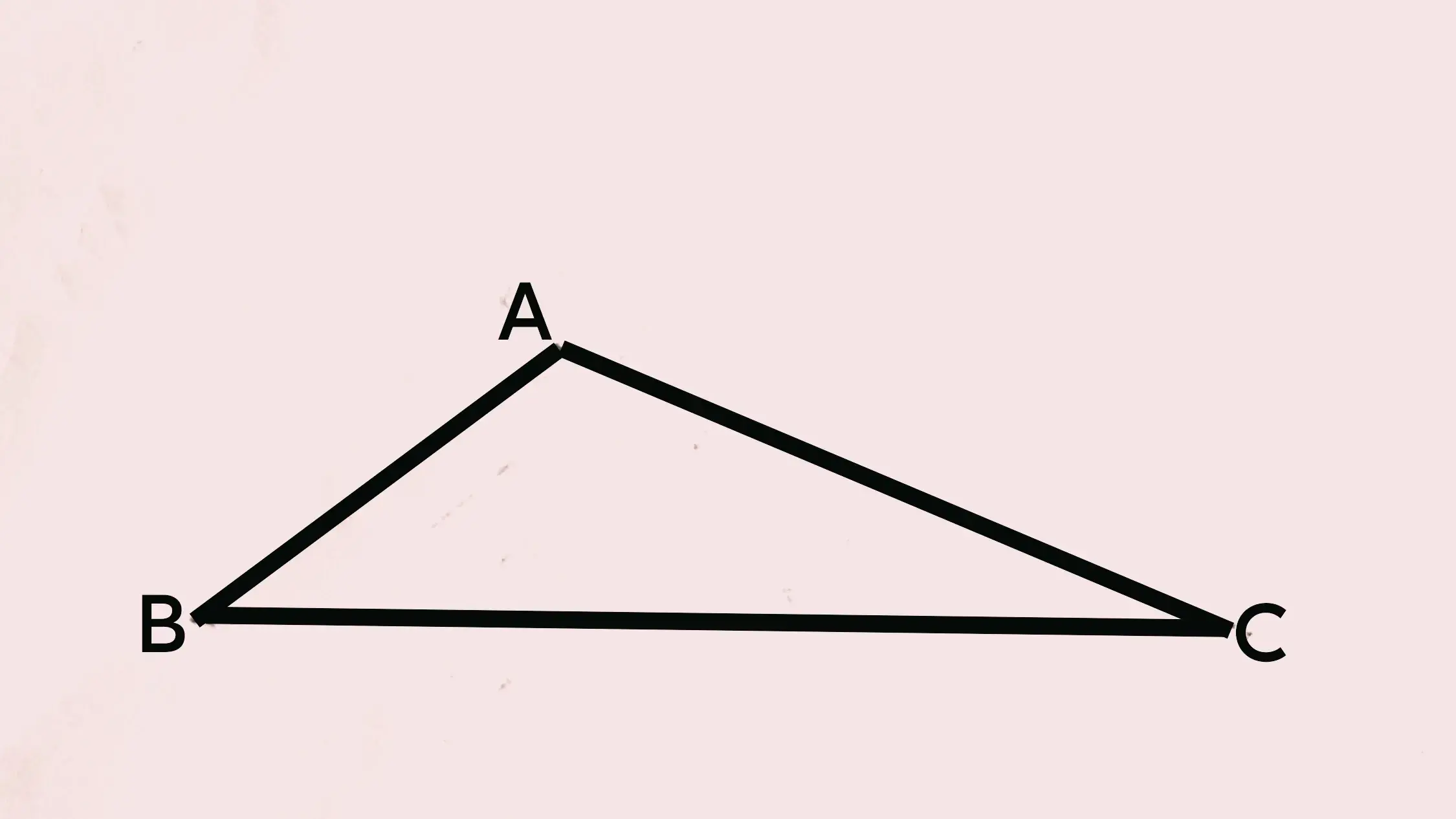
解析：1.初中阶段没有学习余弦定理，虽然知道三角形三边之长，但也无法利用该定理。在此种情况下，就需要构造直角三角形，利用勾股定理去解决问题。

2.对于本题，我们可以过顶点C作BA延长线的垂线CD，垂足为点D，如下图所示。

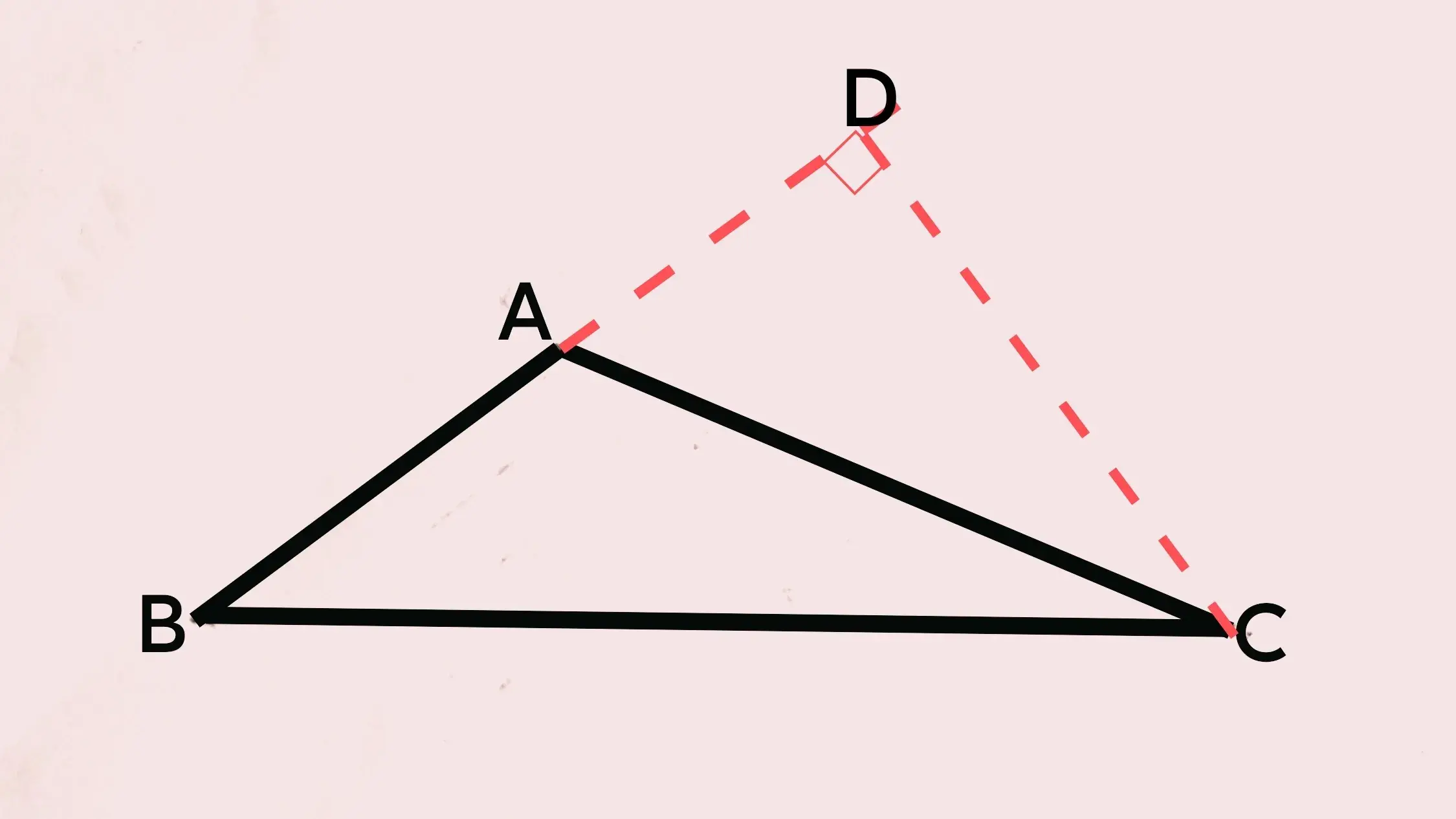
这样我们就构造了两个直角三角形Rt△CDA和Rt△CDB，而且CD是二者的公共边，共可利用它建立等量关系。

令AD=x，则

在Rt△CDA中，

CD²=AC²-AD²

=10²-x²，①

在Rt△CDB中，

CD²=BC²-BD²

=BC²-(BA+AD)²

=14²-(6+x)²，②

由①和②可得：

10²-x²=14²-(6+x)²，

解方程得x=5，

3.在Rt△CDA中，

因为CD=5，AC=10，

所以∠ACD=30⁰，

所以∠CAD=60⁰，

所以∠BAC=180⁰-∠CAD

=180⁰-60⁰

=120⁰。

相关文章